Genetic Algorithms are primarily used in optimization problems of various kinds, but they are frequently used in other application areas as well.
In this section, we list some of the areas in which Genetic Algorithms are frequently used. These are −
Optimization − Genetic Algorithms are most commonly used in optimization problems wherein we have to maximize or minimize a given objective function value under a given set of constraints. The approach to solve Optimization problems has been highlighted throughout the tutorial.
Economics − GAs are also used to characterize various economic models like the cobweb model, game theory equilibrium resolution, asset pricing, etc.
Neural Networks − GAs are also used to train neural networks, particularly recurrent neural networks.
Parallelization − GAs also have very good parallel capabilities, and prove to be very effective means in solving certain problems, and also provide a good area for research.
Image Processing − GAs are used for various digital image processing (DIP) tasks as well like dense pixel matching.
Vehicle routing problems − With multiple soft time windows, multiple depots and a heterogeneous fleet.
Scheduling applications − GAs are used to solve various scheduling problems as well, particularly the time tabling problem.
Machine Learning − as already discussed, genetics based machine learning (GBML) is a niche area in machine learning.
Robot Trajectory Generation − GAs have been used to plan the path which a robot arm takes by moving from one point to another.
Parametric Design of Aircraft − GAs have been used to design aircrafts by varying the parameters and evolving better solutions.
DNA Analysis − GAs have been used to determine the structure of DNA using spectrometric data about the sample.
Multimodal Optimization − GAs are obviously very good approaches for multimodal optimization in which we have to find multiple optimum solutions.
Traveling salesman problem and its applications − GAs have been used to solve the TSP, which is a well-known combinatorial problem using novel crossover and packing strategies.
Advanced Topics
Constrained Optimization Problems
Constrained Optimization Problems are those optimization problems in which we have to maximize or minimize a given objective function value that is subject to certain constraints. Therefore, not all results in the solution space are feasible, and the solution space contains feasible regions as shown in the following image.
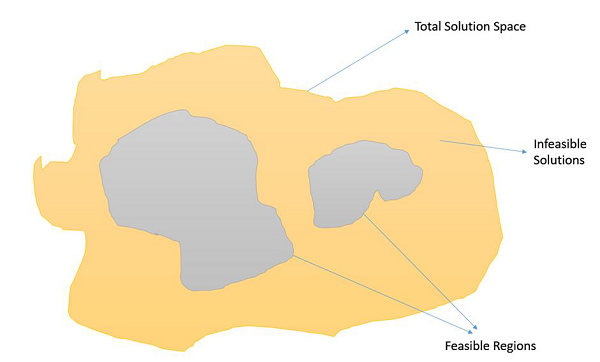
In such a scenario, crossover and mutation operators might give us solutions which are infeasible. Therefore, additional mechanisms have to be employed in the GA when dealing with constrained Optimization Problems.
Some of the most common methods are −
Using penalty functions which reduces the fitness of infeasible solutions, preferably so that the fitness is reduced in proportion with the number of constraints violated or the distance from the feasible region.
Using repair functions which take an infeasible solution and modify it so that the violated constraints get satisfied.
Not allowing infeasible solutions to enter into the population at all.
Use a special representation or decoder functions that ensures feasibility of the solutions.
Basic Theoretical Background
In this section, we will discuss about the Schema and NFL theorem along with the building block hypothesis.
Schema Theorem
Researchers have been trying to figure out the mathematics behind the working of genetic algorithms, and Holland’s Schema Theorem is a step in that direction. Over the year’s various improvements and suggestions have been done to the Schema Theorem to make it more general.
In this section, we don’t delve into the mathematics of the Schema Theorem, rather we try to develop a basic understanding of what the Schema Theorem is. The basic terminology to know are as follows −
A Schema is a “template”. Formally, it is a string over the alphabet = {0,1,*},
where * is don’t care and can take any value.
Therefore, *10*1 could mean 01001, 01011, 11001, or 11011
Geometrically, a schema is a hyper-plane in the solution search space.
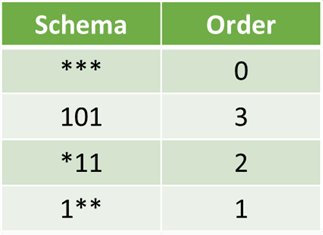
Order of a schema is the number of specified fixed positions in a gene.
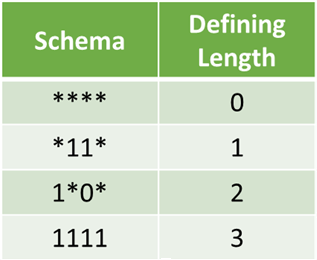
Defining length is the distance between the two furthest fixed symbols in the gene.
The schema theorem states that this schema with above average fitness, short defining length and lower order is more likely to survive crossover and mutation.
Building Block Hypothesis
Building Blocks are low order, low defining length schemata with the above given average fitness. The building block hypothesis says that such building blocks serve as a foundation for the GAs success and adaptation in GAs as it progresses by successively identifying and recombining such “building blocks”.
No Free Lunch (NFL) Theorem
Wolpert and Macready in 1997 published a paper titled "No Free Lunch Theorems for Optimization." It essentially states that if we average over the space of all possible problems, then all non-revisiting black box algorithms will exhibit the same performance.
It means that the more we understand a problem, our GA becomes more problem specific and gives better performance, but it makes up for that by performing poorly for other problems.
GA Based Machine Learning
Genetic Algorithms also find application in Machine Learning. Classifier systems are a form of genetics-based machine learning (GBML) system that are frequently used in the field of machine learning. GBML methods are a niche approach to machine learning.
There are two categories of GBML systems −
The Pittsburg Approach − In this approach, one chromosome encoded one solution, and so fitness is assigned to solutions.
The Michigan Approach − one solution is typically represented by many chromosomes and so fitness is assigned to partial solutions.
It should be kept in mind that the standard issue like crossover, mutation, Lamarckian or Darwinian, etc. are also present in the GBML systems.
Comments
Post a Comment