Genetic Algo Population
Population is a subset of solutions in the current generation. It can also be defined as a set of chromosomes. There are several things to be kept in mind when dealing with GA population −
The diversity of the population should be maintained otherwise it might lead to premature convergence.
The population size should not be kept very large as it can cause a GA to slow down, while a smaller population might not be enough for a good mating pool. Therefore, an optimal population size needs to be decided by trial and error.
The population is usually defined as a two dimensional array of – size population, size x, chromosome size.
Population Initialization
There are two primary methods to initialize a population in a GA. They are −
Random Initialization − Populate the initial population with completely random solutions.
Heuristic initialization − Populate the initial population using a known heuristic for the problem.
It has been observed that the entire population should not be initialized using a heuristic, as it can result in the population having similar solutions and very little diversity. It has been experimentally observed that the random solutions are the ones to drive the population to optimality. Therefore, with heuristic initialization, we just seed the population with a couple of good solutions, filling up the rest with random solutions rather than filling the entire population with heuristic based solutions.
It has also been observed that heuristic initialization in some cases, only effects the initial fitness of the population, but in the end, it is the diversity of the solutions which lead to optimality.
Population Models
There are two population models widely in use −
Steady State
In steady state GA, we generate one or two off-springs in each iteration and they replace one or two individuals from the population. A steady state GA is also known as Incremental GA.
Generational
In a generational model, we generate ‘n’ off-springs, where n is the population size, and the entire population is replaced by the new one at the end of the iteration.
Fitness Function
The fitness function simply defined is a function which takes a candidate solution to the problem as input and produces as output how “fit” our how “good” the solution is with respect to the problem in consideration.
Calculation of fitness value is done repeatedly in a GA and therefore it should be sufficiently fast. A slow computation of the fitness value can adversely affect a GA and make it exceptionally slow.
In most cases the fitness function and the objective function are the same as the objective is to either maximize or minimize the given objective function. However, for more complex problems with multiple objectives and constraints, an Algorithm Designer might choose to have a different fitness function.
A fitness function should possess the following characteristics −
The fitness function should be sufficiently fast to compute.
It must quantitatively measure how fit a given solution is or how fit individuals can be produced from the given solution.
In some cases, calculating the fitness function directly might not be possible due to the inherent complexities of the problem at hand. In such cases, we do fitness approximation to suit our needs.
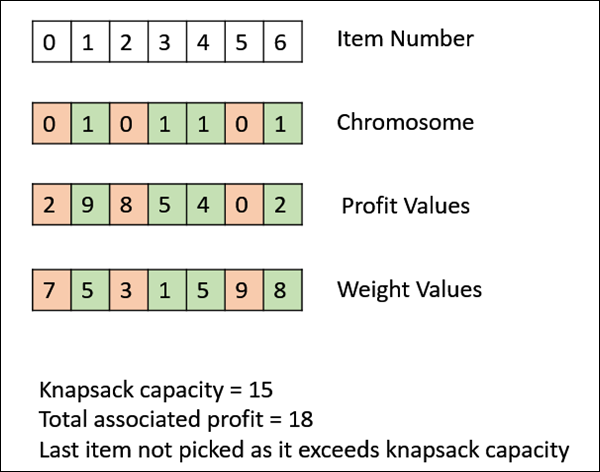
The following image shows the fitness calculation for a solution of the 0/1 Knapsack. It is a simple fitness function which just sums the profit values of the items being picked (which have a 1), scanning the elements from left to right till the knapsack is full.
Parent Selection
Parent Selection is the process of selecting parents which mate and recombine to create off-springs for the next generation. Parent selection is very crucial to the convergence rate of the GA as good parents drive individuals to a better and fitter solutions.
However, care should be taken to prevent one extremely fit solution from taking over the entire population in a few generations, as this leads to the solutions being close to one another in the solution space thereby leading to a loss of diversity. Maintaining good diversity in the population is extremely crucial for the success of a GA. This taking up of the entire population by one extremely fit solution is known as premature convergence and is an undesirable condition in a GA.
Fitness Proportionate Selection
Fitness Proportionate Selection is one of the most popular ways of parent selection. In this every individual can become a parent with a probability which is proportional to its fitness. Therefore, fitter individuals have a higher chance of mating and propagating their features to the next generation. Therefore, such a selection strategy applies a selection pressure to the more fit individuals in the population, evolving better individuals over time.
Consider a circular wheel. The wheel is divided into n pies, where n is the number of individuals in the population. Each individual gets a portion of the circle which is proportional to its fitness value.
Two implementations of fitness proportionate selection are possible −
Roulette Wheel Selection
In a roulette wheel selection, the circular wheel is divided as described before. A fixed point is chosen on the wheel circumference as shown and the wheel is rotated. The region of the wheel which comes in front of the fixed point is chosen as the parent. For the second parent, the same process is repeated.
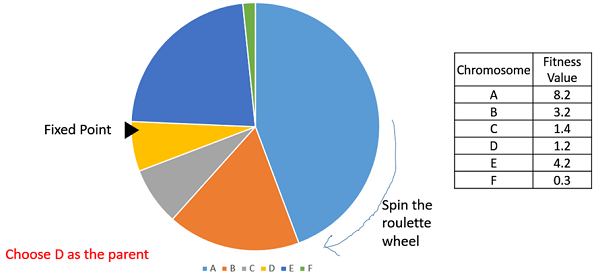
It is clear that a fitter individual has a greater pie on the wheel and therefore a greater chance of landing in front of the fixed point when the wheel is rotated. Therefore, the probability of choosing an individual depends directly on its fitness.
Implementation wise, we use the following steps −
Calculate S = the sum of a finesses.
Generate a random number between 0 and S.
Starting from the top of the population, keep adding the finesses to the partial sum P, till P<S.
The individual for which P exceeds S is the chosen individual.
Stochastic Universal Sampling (SUS)
Stochastic Universal Sampling is quite similar to Roulette wheel selection, however instead of having just one fixed point, we have multiple fixed points as shown in the following image. Therefore, all the parents are chosen in just one spin of the wheel. Also, such a setup encourages the highly fit individuals to be chosen at least once.
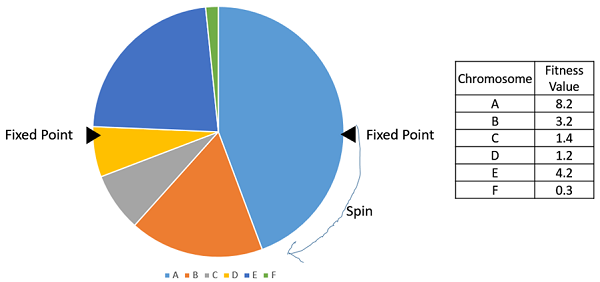
It is to be noted that fitness proportionate selection methods don’t work for cases where the fitness can take a negative value.
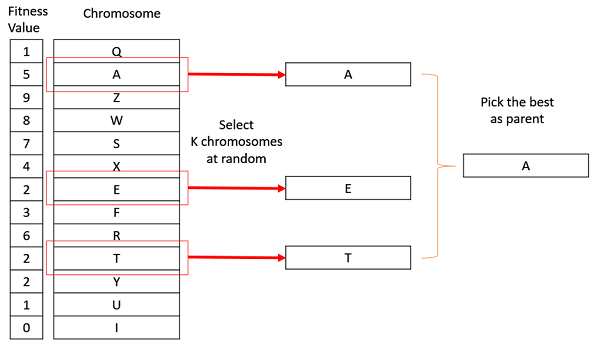
Tournament Selection
In K-Way tournament selection, we select K individuals from the population at random and select the best out of these to become a parent. The same process is repeated for selecting the next parent. Tournament Selection is also extremely popular in literature as it can even work with negative fitness values.
Rank Selection
Rank Selection also works with negative fitness values and is mostly used when the individuals in the population have very close fitness values (this happens usually at the end of the run). This leads to each individual having an almost equal share of the pie (like in case of fitness proportionate selection) as shown in the following image and hence each individual no matter how fit relative to each other has an approximately same probability of getting selected as a parent. This in turn leads to a loss in the selection pressure towards fitter individuals, making the GA to make poor parent selections in such situations.
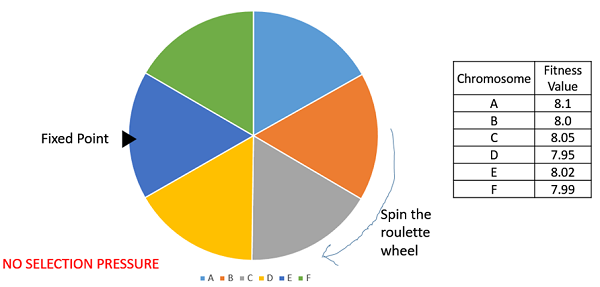
In this, we remove the concept of a fitness value while selecting a parent. However, every individual in the population is ranked according to their fitness. The selection of the parents depends on the rank of each individual and not the fitness. The higher ranked individuals are preferred more than the lower ranked ones.
| Chromosome | Fitness Value | Rank |
|---|---|---|
| A | 8.1 | 1 |
| B | 8.0 | 4 |
| C | 8.05 | 2 |
| D | 7.95 | 6 |
| E | 8.02 | 3 |
| F | 7.99 | 5 |
Random Selection
In this strategy we randomly select parents from the existing population. There is no selection pressure towards fitter individuals and therefore this strategy is usually avoided.
Introduction to Crossover
The crossover operator is analogous to reproduction and biological crossover. In this more than one parent is selected and one or more off-springs are produced using the genetic material of the parents. Crossover is usually applied in a GA with a high probability – pc .
Crossover Operators
In this section we will discuss some of the most popularly used crossover operators. It is to be noted that these crossover operators are very generic and the GA Designer might choose to implement a problem-specific crossover operator as well.
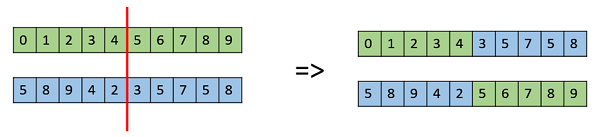
One Point Crossover
In this one-point crossover, a random crossover point is selected and the tails of its two parents are swapped to get new off-springs.
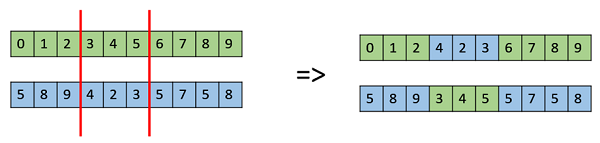
Multi Point Crossover
Multi point crossover is a generalization of the one-point crossover wherein alternating segments are swapped to get new off-springs.
Uniform Crossover
In a uniform crossover, we don’t divide the chromosome into segments, rather we treat each gene separately. In this, we essentially flip a coin for each chromosome to decide whether or not it’ll be included in the off-spring. We can also bias the coin to one parent, to have more genetic material in the child from that parent.
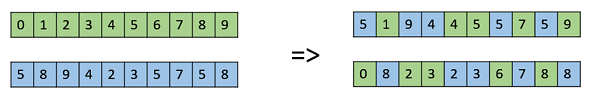
Whole Arithmetic Recombination
This is commonly used for integer representations and works by taking the weighted average of the two parents by using the following formulae −
- Child1 = α.x + (1-α).y
- Child2 = α.x + (1-α).y
Obviously, if α = 0.5, then both the children will be identical as shown in the following image.

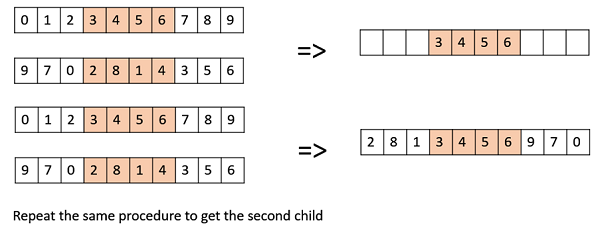
Davis’ Order Crossover (OX1)
OX1 is used for permutation based crossovers with the intention of transmitting information about relative ordering to the off-springs. It works as follows −
Create two random crossover points in the parent and copy the segment between them from the first parent to the first offspring.
Now, starting from the second crossover point in the second parent, copy the remaining unused numbers from the second parent to the first child, wrapping around the list.
Repeat for the second child with the parent’s role reversed.
There exist a lot of other crossovers like Partially Mapped Crossover (PMX), Order based crossover (OX2), Shuffle Crossover, Ring Crossover, etc.
Introduction to Mutation
In simple terms, mutation may be defined as a small random tweak in the chromosome, to get a new solution. It is used to maintain and introduce diversity in the genetic population and is usually applied with a low probability – pm. If the probability is very high, the GA gets reduced to a random search.
Mutation is the part of the GA which is related to the “exploration” of the search space. It has been observed that mutation is essential to the convergence of the GA while crossover is not.
Mutation Operators
In this section, we describe some of the most commonly used mutation operators. Like the crossover operators, this is not an exhaustive list and the GA designer might find a combination of these approaches or a problem-specific mutation operator more useful.
Bit Flip Mutation
In this bit flip mutation, we select one or more random bits and flip them. This is used for binary encoded GAs.
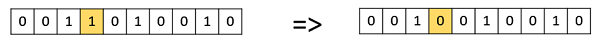
Random Resetting
Random Resetting is an extension of the bit flip for the integer representation. In this, a random value from the set of permissible values is assigned to a randomly chosen gene.
Swap Mutation
In swap mutation, we select two positions on the chromosome at random, and interchange the values. This is common in permutation based encodings.
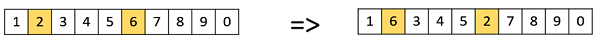
Scramble Mutation
Scramble mutation is also popular with permutation representations. In this, from the entire chromosome, a subset of genes is chosen and their values are scrambled or shuffled randomly.
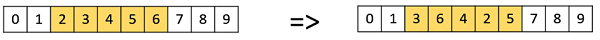
Inversion Mutation
In inversion mutation, we select a subset of genes like in scramble mutation, but instead of shuffling the subset, we merely invert the entire string in the subset.
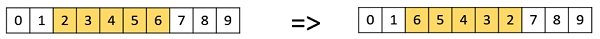
Comments
Post a Comment