Inference in First-Order Logic, Unification, and Resolution in FOL

Inference in First-Order Logic is used to deduce new facts or sentences from existing sentences. Before understanding the FOL inference rule, let's understand some basic terminologies used in FOL.

Substitution:

Substitution is a fundamental operation performed on terms and formulas. It occurs in all inference systems in first-order logic. The substitution is complex in the presence of quantifiers in FOL. If we write F[a/x], so it refers to substitute a constant "a" in place of variable "x".

Note: First-order logic is capable of expressing facts about some or all objects in the universe.

Equality:

First-Order logic does not only use predicate and terms for making atomic sentences but also uses another way, which is equality in FOL. For this, we can use equality symbols which specify that the two terms refer to the same object.

Example: Brother (Chicky) = Ram.

As in the above example, the object referred by the Brother (Chicky) is similar to the object referred by Ram. The equality symbol can also be used with negation to represent that two terms are not the same objects.

Example: ￢(x=y) which is equivalent to x ≠y.

FOL inference rules for quantifier:

As propositional logic we also have inference rules in first-order logic, so following are some basic inference rules in FOL:

• Universal Generalization
• Universal Instantiation
• Existential Instantiation
• Existential introduction

1. Universal Generalization:

• Universal generalization is a valid inference rule which states that if premise P(c) is true for any arbitrary element c in the universe of discourse, then we can have a conclusion as ∀ x P(x).
• It can be represented as: .
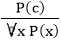• This rule can be used if we want to show that every element has a similar property.
• In this rule, x must not appear as a free variable.

Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.

2. Universal Instantiation:

• Universal instantiation is also called as universal elimination or UI is a valid inference rule. It can be applied multiple times to add new sentences.
• The new KB is logically equivalent to the previous KB.
• As per UI, we can infer any sentence obtained by substituting a ground term for the variable.
• The UI rule state that we can infer any sentence P(c) by substituting a ground term c (a constant within domain x) from ∀ x P(x) for any object in the universe of discourse.
• It can be represented as:.

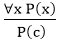Example:1.

IF "Every person like ice-cream"=> ∀x P(x) so we can infer that
"Erra likes ice-cream" => P(c)

Example: 2.

Let's take a famous example,

"All politicians who are greedy are Evil." So let our knowledge base contains this detail as in the form of FOL:

∀x politician(x) ∧ greedy (x) → Evil (x),

So from this information, we can infer any of the following statements using Universal Instantiation:

• politician(Chicky) ∧ Greedy (Chicky) → Evil (Chicky),
• politician(Rahul) ∧ Greedy (Rahul) → Evil (Rahul),
• politician(Father(Chicky)) ∧ Greedy (Father(Chicky)) → Evil (Father(Chicky)),

3. Existential Instantiation:

• Existential instantiation is also called as Existential Elimination, which is a valid inference rule in first-order logic.
• It can be applied only once to replace the existential sentence.
• The new KB is not logically equivalent to old KB, but it will be satisfiable if old KB was satisfiable.
• This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
• The restriction with this rule is that c used in the rule must be a new term for which P(c ) is true.
• It can be represented as:

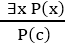
Example:

From the given sentence: ∃x Crown(x) ∧ OnHead(x, Erra),

So we can infer: Crown(K) ∧ OnHead( K, Erra), as long as K does not appear in the knowledge base.

• The above used K is a constant symbol, which is called Skolem constant.
• The Existential instantiation is a special case of Skolemization process.

4. Existential introduction

• An existential introduction is also known as an existential generalization, which is a valid inference rule in first-order logic.
• This rule states that if there is some element c in the universe of discourse which has a property P, then we can infer that there exists something in the universe which has the property P.
• It can be represented as: 
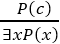
• Example: Let's say that,
  "Erra got good marks in English."
  "Therefore, someone got good marks in English."

Generalized Modus Ponens Rule:

For the inference process in FOL, we have a single inference rule which is called Generalized Modus Ponens. It is lifted version of Modus ponens.

Generalized Modus Ponens can be summarized as, " P implies Q and P is asserted to be true, therefore Q must be True."

According to Modus Ponens, for atomic sentences pi, pi', q. Where there is a substitution θ such that SUBST (θ, pi',) = SUBST(θ, pi), it can be represented as:

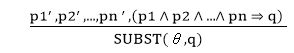
Example:

We will use this rule for politicians are evil, so we will find some x such that x is politician, and x is greedy so we can infer that x is evil.

1. Here let say, p1' is politician(chicky)        p1 is politician(x)  
2. p2' is Greedy(y)                       p2 is Greedy(x)  
3. θ is {x/Chicky, y/Chicky}                  q is evil(x)  
4. SUBST(θ,q).                                               

What is Unification?

• Unification is a process of making two different logical atomic expressions identical by finding a substitution. Unification depends on the substitution process.
• It takes two literals as input and makes them identical using substitution.
• Let Ψ₁ and Ψ₂ be two atomic sentences and 𝜎 be a unifier such that, Ψ₁𝜎 = Ψ₂𝜎, then it can be expressed as UNIFY(Ψ₁, Ψ₂).
• Example: Find the MGU for Unify{Politician(x), Politician(Chicky)}

Let Ψ₁ = Politician(x), Ψ₂ = Politician(Chicky),

Substitution θ = {Chicky/x} is a unifier for these atoms and applying this substitution, and both expressions will be identical.

• The UNIFY algorithm is used for unification, which takes two atomic sentences and returns a unifier for those sentences (If any exist).
• Unification is a key component of all first-order inference algorithms.
• It returns fail if the expressions do not match with each other.
• The substitution variables are called Most General Unifier or MGU.

E.g. Let's say there are two different expressions, P(x, y), and P(a, f(z)).

In this example, we need to make both above statements identical to each other. For this, we will perform the substitution.

            P(x, y)......... (i)
            P(a, f(z))......... (ii)

• Substitute x with a, and y with f(z) in the first expression, and it will be represented as a/x and f(z)/y.
• With both the substitutions, the first expression will be identical to the second expression and the substitution set will be: [a/x, f(z)/y].

Conditions for Unification:

Following are some basic conditions for unification:

• Predicate symbol must be same, atoms or expression with different predicate symbol can never be unified.
• Number of Arguments in both expressions must be identical.
• Unification will fail if there are two similar variables present in the same expression.

Unification Algorithm:

Algorithm: Unify(Ψ₁, Ψ₂)

Step. 1: If Ψ1 or Ψ2 is a variable or constant, then:
	a) If Ψ1 or Ψ2 are identical, then return NIL. 
	b) Else if Ψ1is a variable, 
		a. then if Ψ1 occurs in Ψ2, then return FAILURE
		b. Else return { (Ψ2/ Ψ1)}.
	c) Else if Ψ2 is a variable, 
		a. If Ψ2 occurs in Ψ1 then return FAILURE,
		b. Else return {( Ψ1/ Ψ2)}. 
	d) Else return FAILURE. 
Step.2: If the initial Predicate symbol in Ψ1 and Ψ2 are not same, then return FAILURE.
Step. 3: IF Ψ1 and Ψ2 have a different number of arguments, then return FAILURE.
Step. 4: Set Substitution set(SUBST) to NIL. 
Step. 5: For i=1 to the number of elements in Ψ1. 
	a) Call Unify function with the ith element of Ψ1 and ith element of Ψ2, and put the result into S.
	b) If S = failure then returns Failure
	c) If S ≠ NIL then do,
		a. Apply S to the remainder of both L1 and L2.
		b. SUBST= APPEND(S, SUBST). 
Step.6: Return SUBST. 

Implementation of the Algorithm

Step.1: Initialize the substitution set to be empty.

Step.2: Recursively unify atomic sentences:

1. Check for Identical expression match.
2. If one expression is a variable v_i, and the other is a term t_i which does not contain variable v_i, then:
   1. Substitute t_i / v_i in the existing substitutions
   2. Add t_i /v_i to the substitution setlist.
   3. If both the expressions are functions, then function name must be similar, and the number of arguments must be the same in both the expression.

For each pair of the following atomic sentences find the most general unifier (If exist).

1. Find the MGU of {p(f(a), g(Y)) and p(X, X)}

            Sol: S₀ => Here, Ψ₁ = p(f(a), g(Y)), and Ψ₂ = p(X, X)
                  SUBST θ= {f(a) / X}
                  S1 => Ψ₁ = p(f(a), g(Y)), and Ψ₂ = p(f(a), f(a))
                  SUBST θ= {f(a) / g(y)}, Unification failed.

Unification is not possible for these expressions.

2. Find the MGU of {p(b, X, f(g(Z))) and p(Z, f(Y), f(Y))}

Here, Ψ₁ = p(b, X, f(g(Z))) , and Ψ₂ = p(Z, f(Y), f(Y))
S₀ => { p(b, X, f(g(Z))); p(Z, f(Y), f(Y))}
SUBST θ={b/Z}

S₁ => { p(b, X, f(g(b))); p(b, f(Y), f(Y))}
SUBST θ={f(Y) /X}

S₂ => { p(b, f(Y), f(g(b))); p(b, f(Y), f(Y))}
SUBST θ= {g(b) /Y}

S₂ => { p(b, f(g(b)), f(g(b)); p(b, f(g(b)), f(g(b))} Unified Successfully.
And Unifier = { b/Z, f(Y) /X , g(b) /Y}.

3. Find the MGU of {p (X, X), and p (Z, f(Z))}

Here, Ψ₁ = {p (X, X), and Ψ₂ = p (Z, f(Z))
S₀ => {p (X, X), p (Z, f(Z))}
SUBST θ= {X/Z}
              S1 => {p (Z, Z), p (Z, f(Z))}
SUBST θ= {f(Z) / Z}, Unification Failed.

Hence, unification is not possible for these expressions.

4. Find the MGU of UNIFY(prime (11), prime(y))

Here, Ψ₁ = {prime(11) , and Ψ₂ = prime(y)}
S₀ => {prime(11) , prime(y)}
SUBST θ= {11/y}

S₁ => {prime(11) , prime(11)} , Successfully unified.
              Unifier: {11/y}.

5. Find the MGU of Q(a, g(x, a), f(y)), Q(a, g(f(b), a), x)}

Here, Ψ₁ = Q(a, g(x, a), f(y)), and Ψ₂ = Q(a, g(f(b), a), x)
S₀ => {Q(a, g(x, a), f(y)); Q(a, g(f(b), a), x)}
SUBST θ= {f(b)/x}
S₁ => {Q(a, g(f(b), a), f(y)); Q(a, g(f(b), a), f(b))}

SUBST θ= {b/y}
S₁ => {Q(a, g(f(b), a), f(b)); Q(a, g(f(b), a), f(b))}, Successfully Unified.

Unifier: [a/a, f(b)/x, b/y].

6. UNIFY(knows(Ram, x), knows(Ram, Chicky))

Here, Ψ₁ = knows(Ram, x), and Ψ₂ = knows(Ram, Chicky)
S₀ => { knows(Ram, x); knows(Ram, Chicky)}
SUBST θ= {Chicky/x}
S₁ => { knows(Ram, Chicky); knows(Ram, Chicky)}, Successfully Unified.
Unifier: {Chicky/x}.

Resolution

Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by a Mathematician John Alan Robinson in the year 1965.

Resolution is used, if there are various statements are given, and we need to prove a conclusion of those statements. Unification is a key concept in proofs by resolutions. Resolution is a single inference rule which can efficiently operate on the conjunctive normal form or clausal form.

Clause: Disjunction of literals (an atomic sentence) is called a clause. It is also known as a unit clause.

Conjunctive Normal Form: A sentence represented as a conjunction of clauses is said to be conjunctive normal form or CNF.

Note: To better understand this topic, firstly learns the FOL in AI.

The resolution inference rule:

The resolution rule for first-order logic is simply a lifted version of the propositional rule. Resolution can resolve two clauses if they contain complementary literals, which are assumed to be standardized apart so that they share no variables.

Where l_i and m_j are complementary literals.

This rule is also called the binary resolution rule because it only resolves exactly two literals.

Example:

We can resolve two clauses which are given below:

[Animal (g(x) V Loves (f(x), x)]       and       [￢ Loves(a, b) V ￢Kills(a, b)]

Where two complimentary literals are: Loves (f(x), x) and ￢ Loves (a, b)

These literals can be unified with unifier θ= [a/f(x), and b/x] , and it will generate a resolvent clause:

[Animal (g(x) V ￢ Kills(f(x), x)].

Steps for Resolution:

1. Conversion of facts into first-order logic.
2. Convert FOL statements into CNF
3. Negate the statement which needs to prove (proof by contradiction)
4. Draw resolution graph (unification).

To better understand all the above steps, we will take an example in which we will apply resolution.

Example:

1. John likes all kind of food.
2. Apple and vegetable are food
3. Anything anyone eats and not killed is food.
4. Anil eats peanuts and still alive
5. Harry eats everything that Anil eats.
   Prove by resolution that:
6. John likes peanuts.

Step-1: Conversion of Facts into FOL

In the first step we will convert all the given statements into its first order logic.

Step-2: Conversion of FOL into CNF

In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.

• Eliminate all implication (→) and rewrite
  1. ∀x ¬ food(x) V likes(John, x)
  2. food(Apple) Λ food(vegetables)
  3. ∀x ∀y ¬ [eats(x, y) Λ ¬ killed(x)] V food(y)
  4. eats (Anil, Peanuts) Λ alive(Anil)
  5. ∀x ¬ eats(Anil, x) V eats(Harry, x)
  6. ∀x¬ [¬ killed(x) ] V alive(x)
  7. ∀x ¬ alive(x) V ¬ killed(x)
  8. likes(John, Peanuts).
• Move negation (¬)inwards and rewrite
  1. ∀x ¬ food(x) V likes(John, x)
  2. food(Apple) Λ food(vegetables)
  3. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)
  4. eats (Anil, Peanuts) Λ alive(Anil)
  5. ∀x ¬ eats(Anil, x) V eats(Harry, x)
  6. ∀x ¬killed(x) ] V alive(x)
  7. ∀x ¬ alive(x) V ¬ killed(x)
  8. likes(John, Peanuts).
• Rename variables or standardize variables
  1. ∀x ¬ food(x) V likes(John, x)
  2. food(Apple) Λ food(vegetables)
  3. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)
  4. eats (Anil, Peanuts) Λ alive(Anil)
  5. ∀w¬ eats(Anil, w) V eats(Harry, w)
  6. ∀g ¬killed(g) ] V alive(g)
  7. ∀k ¬ alive(k) V ¬ killed(k)
  8. likes(John, Peanuts).
• Eliminate existential instantiation quantifier by elimination.
  In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.
• Drop Universal quantifiers.
  In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.
  1. ¬ food(x) V likes(John, x)
  2. food(Apple)
  3. food(vegetables)
  4. ¬ eats(y, z) V killed(y) V food(z)
  5. eats (Anil, Peanuts)
  6. alive(Anil)
  7. ¬ eats(Anil, w) V eats(Harry, w)
  8. killed(g) V alive(g)
  9. ¬ alive(k) V ¬ killed(k)
  10. likes(John, Peanuts).

Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.

• Distribute conjunction ∧ over disjunction ¬.
  This step will not make any change in this problem.

Step-3: Negate the statement to be proved

In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)

Step-4: Draw Resolution graph:

Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:

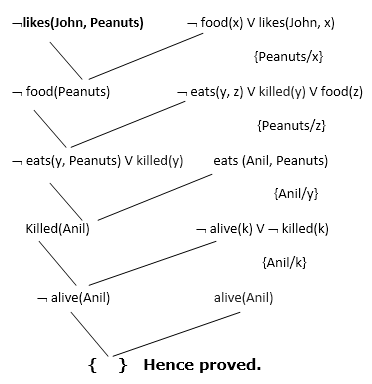
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.

Explanation of Resolution graph:

• In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(canceled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
• In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (canceled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
• In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
• In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
• In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.

Anurag Rana